README

Pure double & double-double floating point arithmetic functions with strict error bounds

This library is only possible through the research of Mioara Joldes, Jean-Michel Muller, Valentina Popescu, Tight and rigourous error bounds for basic building blocks of double-word arithmetic

Documentation

Overview

Double-double precision floating point operators (similar to quad precision)
Each function documents a strict error bound (see research [1] below)
Optimized for speed (see benchmark below)
Operators include: +, -, *, /, √, abs, <, >, ===, min, max, etc.
Operators mixing double and double-doubles are also included, e.g. ddAddDouble (for adding a double to a double-double)
Error free double precision operators also included, e.g. twoProduct (for calculating the exact result of multiplying two doubles)
No classes ⇒ a double-double is simply a length 2 Number array, e.g.

import { twoSum } from 'double-double';
// Specified directly (low order double first)
const a = [-4.357806199228875e-10, 11_638_607.274152497];
// ...or more usually from an earlier calculation
const b = twoSum(213.456, 111.111);  // => [-1.4210854715202004e-14, 324.567] (completely error-free)

All functions are pure, e.g.

// using `a` and `b` as defined above (ddAddDd => double-double + double-double)
const c = ddAddDd(a,b);  // => [-2.42072459299969e-10, 11638931.841152497]

No dependencies

Installation

npm install double-double

This package is ESM only and can be used in Node.js (or in a browser when bundled using e.g. Webpack).

Additionally, self-contained ECMAScript Module (ESM) files index.module.js and index.module.min.js in the ./browser folder is provided.

Or, if you need a legacy browser script there is also index.js and index.min.js in the ./browser folder. Either script exposes a global variable called doubleDouble.

See full examples below.

A Practical example (Node.js)

Let's say you want to calculate the determinant of the following 2x2 matrix:
┌─ ─┐
│ A B │
│ C D │
└─ ─┘

In other words, let's say you want to calculate (A*D - B*C).

Let's further assume:

const A = 11.13;               // A is double precision ieee754 floating point number
const B = 8.664;               // ...
const C = 3.6329224376731304;  // ...
const D = 2.828;               // ...

In double precision the calculation is easy:

const d = A*D - B*C  // => 0

but gives the completely wrong answer of 0 due to round-off combined with catastrophic cancellation.

Using double-double precision gives:

import { twoProduct, ddDiffDd } from 'double-double';

// dd = A*D - B*C
const dd = ddDiffDd(twoProduct(A,D), twoProduct(B,C)); // => [0, -9.743145041148111e-17]

// The final answer can easily be rounded to the 'nearest' double:
const d1 = dd[0] + dd[1];  // => -9.743145041148111e-17
// or, alternatively truncated
const d2 = dd[1];  // => -9.743145041148111e-17

So the final result (after rounding back to double precision) is -9.743145041148111e-17 which is the exact result (i.e. no error) in this case.

As another example, if we take:

const A = 0.13331;
const B = 8.668;
const C = 3.609;
const D = 2.885;

we get the result (again after rounding to double precision) to be:

const d2 = -30.898212649999998;

Let us calculate an absolute error bound of the above? (This may or may not be important depending on the application.)

The documentation of ddDiffDd states:

Relative error bound: 3u^2 + 13u^3, i.e. fl(a-b) = (a-b)(1+ϵ), where ϵ <= 3u^2 + 13u^3, u = 0.5 * Number.EPSILON

For simplicity we incorporate the 3rd order term of 13u^3 in the 2nd order term, i.e. 3u^2 becomes 4u^2 === 4.930380657631324e-32 < 5e-32. (Note that the fl() function above is not the usual one in double precision, but instead represents a double-double precision calculation. Also, fl(a - b) is often denoted by a ⊖ b as for example in What Every Computer Scientist Should Know About Floating-Point Arithmetic.)

The maximum absolute error bound is then |a - b||ϵ| = |0.13331*2.885 - 8.668*3.609||5e-32| = 1.5449106325000001e-30 where A, B, C and D is as given previously. (The actual error is 4.930380657631324e-32)

In other words the calculation of dd above as a double-double represented as the length 2 array [6.3219416368554e-16, -30.898212649999998] with exact value 6.3219416368554e-16 + -30.898212649999998 is accurate up to roughly the 30th digit. (Typically the calculations will be more complex such as when the matrix is, say, 3x3 and the final result is often truncated to double precision.)

Usage

Node.js

// @filename: `test.mjs` (or `test.js` if { "type": "module" } is specified in your package.json)
import { ddAddDd } from 'double-double';  // `ddAddDd` returns the sum of two double-doubles 

const dd1 = [-4.357806199228875e-10, 11638607.274152497];  // some double-double
const dd2 = [4.511949494578893e-11, -2797357.2918064594];  // another double-double

const r1 = ddAddDd(dd1,dd2);  // sum the two double-doubles
const r2 = [-3.906611249770986e-10, 8841249.982346037];  // the correct result

if (r1[0] === r2[0] && r1[1] === r2[1]) {
    console.log('success! 😁');  // we should get to here!
} else {
    console.log('failure! 😥');  // ...and not here
}

Browsers - ESM - (Chrome 61+, Safari 11+, Firefox 60+, Opera 48+, Edge 16+, Internet Explorer)

<!doctype html>

<html lang="en">
<head>
    <script type="module">
        import { ddAddDd } from "./node_modules/double-double/browser/index.module.min.js";

        const dd1 = [-4.357806199228875e-10, 11638607.274152497];  // some double-double
        const dd2 = [4.511949494578893e-11, -2797357.2918064594];  // another double-double

        const r1 = ddAddDd(dd1,dd2);  // sum the two double-doubles
        const r2 = [-3.906611249770986e-10, 8841249.982346037];  // the correct result

        if (r1[0] === r2[0] && r1[1] === r2[1]) {
            console.log('success! 😁');  // we should get to here!
        } else {
            console.log('failure! 😥');  // ...and not here
        }
    </script>
</head>

<body>Check the console.</body>

</html>

Browsers (older) - Legacy Scripts

<!doctype html>

<html lang="en">
<head>
    <script src="./browser/index.min.js"></script>
    <script>
        const { ddAddDd } = doubleDouble;

        const dd1 = [-4.357806199228875e-10, 11638607.274152497];  // some double-double
        const dd2 = [4.511949494578893e-11, -2797357.2918064594];  // another double-double

        const r1 = ddAddDd(dd1,dd2);  // sum the two double-doubles
        const r2 = [-3.906611249770986e-10, 8841249.982346037];  // the correct result

        if (r1[0] === r2[0] && r1[1] === r2[1]) {
            console.log('success! 😁');  // we should get to here!
        } else {
            console.log('failure! 😥');  // ...and not here
        }
    </script>
</head>

<body>Check the console.</body>

</html>

Bundlers (Webpack, Rollup, ...)

Webpack will be taken as an example here.

Since your webpack config file might still use CommonJS you must rename webpack.config.js to webpack.config.cjs.

If you are using TypeScript:

Since this is an ESM only library you must use resolve-typescript-plugin (at least until webpack catches up with ESM?) in your webpack.config.cjs file.

npm install --save-dev resolve-typescript-plugin

and follow the instructions given at resolve-typescript-plugin.

Additionally, follow this guide.

❗Important❗

When using bundlers:
import { operators } from 'double-double'
and then later in the code get the functions you need, e.g.:
const { ddAddDd as add, twoProduct, /* etc. */ } = operators;
as opposed to importing the operators directly.

This will increase performance roughly 5 times!

Why? Because Webpack (and Rollup) exports functions using getters that gets invoked on every function call adding a big overhead and slowing down each function. This is not an issue if the code is not bundled, e.g. when using Node.js.

Research

The following research / books / lectures have been used or are directly relevant to this library (especially the first two):

Benchmark

benchmark

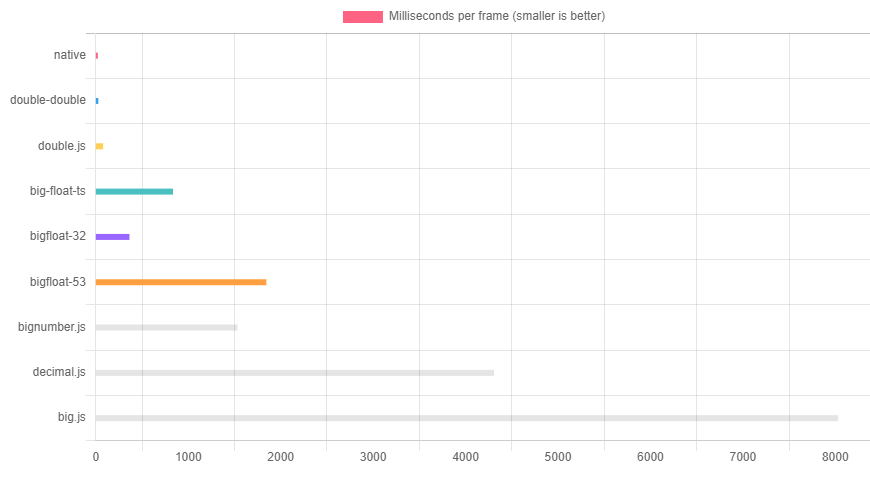
Similar libraries in Javascript / TypeScript

double.js

License

MIT

Usage no npm install needed!